1. Identificar las dimensiones de la sección rectangular: ancho (b) y altura (h). 2. Calcular el momento de inercia de área utilizando la fórmula específica para un rectángulo: I = (b * h^3) / 12. Donde: - I es el momento de inercia de área. - b es el ancho de la sección rectangular.. artículo de lista de Wikimedia / De Wikipedia, la enciclopedia encyclopedia. Este anexo contiene una lista de momentos de inercial para áreas. El momento de inercia de área o segundo momento de área tiene como unidad de medida [longitud] 4 y no debe ser confundido con el momento de inercia másico (cuyas unidades son [masa]· [longitud] 2.

Momentos de inercia de áreas Mecánica racional IRectángulo Círculo Media Parabólica

ING. Elías Malavé Areas, Centroides y Momentos de Inercia

Cómo calcular MOMENTO de INERCIA de figuras COMPUESTAS 🔶 YouTube

Tabela para cálculo de momentos de inércia

Cálculo del MOMENTO DE INERCIA DE UN CILÍNDRO HUECO Y SÓLIDO POR INTEGRACIÓN ejercicio resuelto

Cálculo del centroide y momento de inercia con respecto al área YouTube

Estática Centro de Gravedad y Momentos de Inercia Primer Momento de Áreas y Líneas YouTube

Momento de Inercia de Áreas PDF

Cálculo del MOMENTO DE INERCIA(Teorema de Steiner/Ejes centroidales) Ejem.01 YouTube
Cálculo del Momento de Inercia en Cuerpo Extensos Calculisto Resúmenes y Clases de Cálculo

Cómo Calcular el Momento de Inercia de Figuras Compuestas 👍 Ejemplos y Ejercicios Resueltos

Momento de Inércia Como Calcular ResMat YouTube

Momentos de Inercia de Area Integral Objetos matemáticos

Tablas de Momentos de Inercia (Por Volumenes y Areas) PDF

Momentos de inercia para Áreas compuestas YouTube
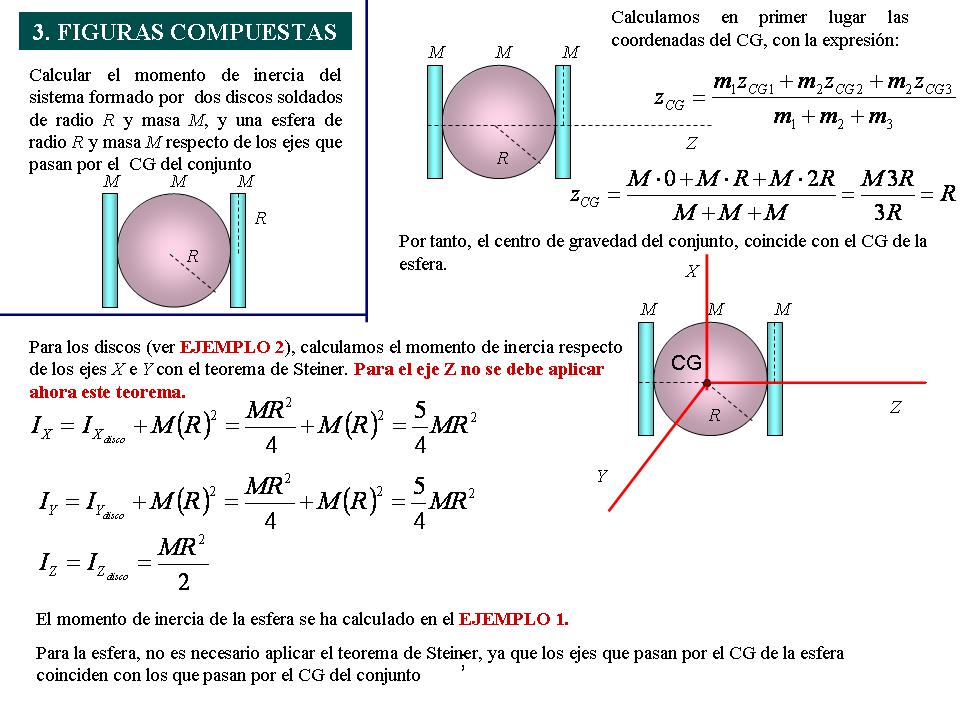
MOMENTOS DE INERCIA FIGURAS COMPUESTAS

Momento de Inercia usando Integrales Dobles de una Lámina Plana YouTube

Cálculo del momento de inercia (Teorema de Steiner/Ejes centroidales) Ejem.02 YouTube
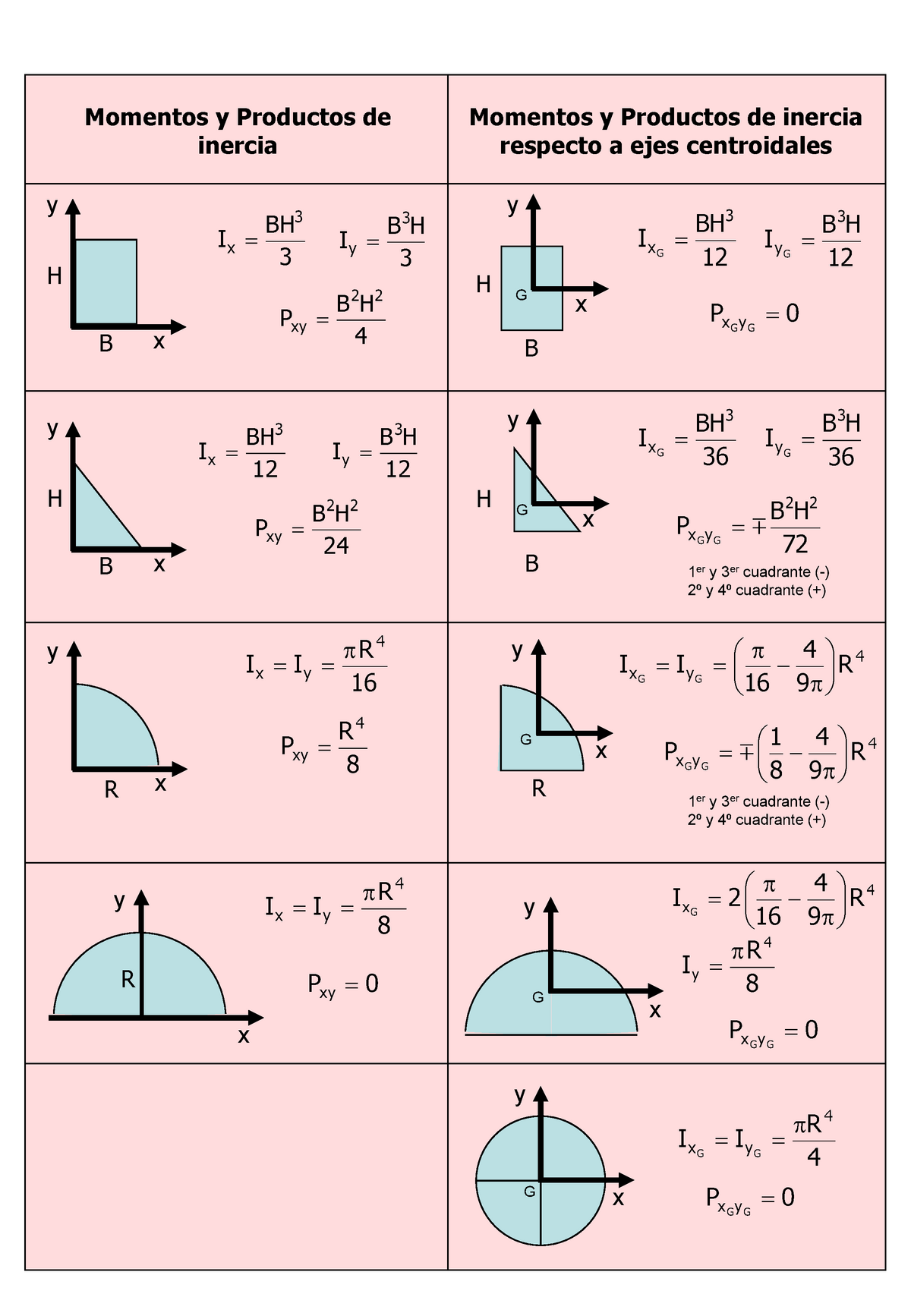
Momento De Inercia Tabela SOLOLEARN

Fórmulas para encontrar el momento de inercia YuBrain
Para el área completa, los momentos de inercia son: Estas integrales, conocidas como los momentos rectangulares de inercia del área A, se pueden evaluar con facilidad si se selecciona a dA como una tira delgada paralela a uno de los ejes coordenados. Aquí, r es la distancia perpendicular desde el polo (eje z) hasta el elemento dA.. Ejemplos de cálculo. Un objeto extendido, como una barra, disco, esfera u otro, cuya densidad ρ es constante y sabiendo que la densidad es el cociente masa - volumen, el diferencial de masa dm se escribe como: ρ = dm/dV → dm = ρdV. Sustituyendo en la integral para el momento de inercia, tenemos: I = ∫r2 ρdV = ρ ∫r2dV.